▼The Racket School of Semantics and Languages 2017
►1 From the Lambda Calculus to Redex
On this page:
1.1 Workshop Goals
1.2 Theory:   Trees, Substitution
1.3 Redex:   Languages, Scope, and Substitution
1.4 Theory:   Laws of Calculation
1.5 Redex:   Contexts, Reductions, Graphs
1.6 Theory:   From Calculation to Programming Languages
1.7 Redex:   Evaluators for Programming Languages
1.8 Summary:   Theory
1.9 Summary:   Redex
6.10.0.2
    ← prev  up  next → 

1 From the Lambda Calculus to Redex

Goals

— What you will learn, how this might be useful

— Basic Theory: reductions and calculations, eval

— from Theory to Redex

1.1 Workshop Goals

Monday is about the very basics of operational models and semantics of functional programming languages, that is, so-called syntactic theories.

On Tuesday and Wednesday we will expand the coverage to imperative languages, and you will learn to investigate the relationship between syntax and semantics. Practitioners may take away ideas for approaching new languages, instructors will see an entirely new way of teaching a course on programming languages.

Thursday will be dedicated to building languages in Racket.

Friday will tie together the Redex modeling approaches and the language building approaches.

This summer school cannot possible cover everything in the Racket school of programming languages. For example, we will not show you how to work with abstract machines. We will not show you how to create Racket languages that use conventional syntax. And we will not work on performance issues of models or language creation. By covering the wide spectrum of ideas, however, we hope you get an idea of what Racket and its eco-system offers and that you will take some time in the future to explore this world in some depth.

1.2 Theory: Trees, Substitution

Terms vs Trees The lambda calculus: most familiar, still misunderstood

e = x | (λx.e) | (e e)

Terms vs trees, abstract over concrete syntax. Don’t ever think of (λx.(x (λy.y))) as a string or sequence of chars; always think of it as a tree:

      λx.

      |

     app

     / \

    x   λy.

         |

         y

Substitution From 8th grade math we know that functions are about “plugging values in for variables.” In our world, this is called substitution. Notation:

 e[x <- e’]

pronounced: e with x replaced by e’

Substitution is tree surgery. But there are two ways to think about it:

 (λy.x)[x <- y] == λy.y

if taken literally.

But λy.x is like a constant function f(y) = x. The result, however, is a function that depends on its variable f(y) = y.

Here is the other way:

 (λy.x)[x <- y] == (λz.x)[x <- y] == λz.y

Understand scope. Preserve bindings. And this is indeed the first task of PL people, too. There are several ways to understand scope:

1.3 Redex: Languages, Scope, and Substitution

(define-language Lambda1
  (e ::= x
         (lambda (x) e)
         (e e))
  (x ::= variable-not-otherwise-mentioned))

Here are the terms from above:
(define e1 (term (lambda (x) y)))
(define e2 (term (lambda (z) y)))
 
(default-language Lambda1)
 
(term (substitute ,e1 y x))
(term (substitute ,e2 y x))
And these are the results we don’t want. Because we did not specify scope aka binding structure of our language.

Let’s fix that:
(define-language Lambda
  (e ::= x
         (lambda (x) e)
         (e e))
  (x ::= variable-not-otherwise-mentioned)
  #:binding-forms
  (lambda (x) e #:refers-to x))
 
(default-language Lambda)
(term (substitute ,e1 y x))
(term (substitute ,e2 y x))
And now it all works out.

Discuss alpha-equivalent?

1.4 Theory: Laws of Calculation

What are doing when we calculate? What do we mean when we write =, as in,

3 * (1 + 1) = 3 * 2 = 6

We teach children that this is the “truth” but we can also just view = or “computes to” as a relationship between terms. So 3 * (1 + 1) is a term, meaning a tree in our world:

      *

     / \

    3   +

       / \

      1   1

And the next term in the series is

      *

     / \

    3   2

Which just says that “calculation is a relationship on terms.”

The lambda calculus is for calculating with functions instead of numbers. So we need a relation that models the fundamental idea of function application. Here are three of them:

  •  ((λx.e) e’) beta-x e

    This one is totally weird. Functions always ignore their argument. That is not what we want.

Here is what we want:

    f(x) = 3 * (x + 1)

    ------------------

    f(1) = 3 * (1 + 1)

         = 3 * 2

         = 6

  •  ((λx.e) e’) beta-y e[x <- e’]

    This one is better than the first but if we add arithmetic, odd things happen:

        g(x) = 42

        ------------------

        g(1/0) = 42

    Do we really want calculations to ignore errors? Do developers really want their PL to throw away an erroneous computation?

    Not even the Lambda Calculus inventors were sure about this. They dabbled in alternatives (for example the λI calculus) but could not resolve the problem.

  •  ((λx.e) (λx.e’) ) beta-z e[x <- (λx.’e) ]

    This last relation resolves this issue by restricting the argument of a function to be a function. In a world where everything is a function, this seems okay.

In the past 50 years, y has become known as “call by name” (as in Algol 60 or Simula 67) and z has become known as “call by value” (as in Pascal or Java).

The basic relation is not enough to calculate. Every kid knows that you can always “substitute equals for equals” in a term. So if we wish to understand calculation from this fundamental perspective, we need to generalize the basic relation to one that “calculates wherever you want.”

Obviously we need to add reflexivity (e = e), symmetry (e = e’ then e’ = e), and transitivity (e = e’ and e’ = e” then e = e”).

But we also need to be able to do this anywhere in the tree. We use contexts to express this idea. A context is result of removing a sub-tree from a term term:

C = [] | (λx.C) | (C e) | (e C)

[] is called a hole and the only operation on contexts is to fill the hole with a tree, i.e., to graft a tree onto the pruned branch:

C = (λx.[]) and e = (λy.x), then C[e] = (λx.(λy.x))

Yes! Grafting a tree onto a context captures variables. That’s intentional. Watch:

e = (λz.(λy.z)) x.

With beta-y, we get

e = (λy.x).

But if this calculation takes place in some context

C = (λx.[])

then we want to calculate like this:

C[(λz.(λy.z)) x] = C[(λy.x)]

regardless of what C is.

In general, if e = e’, then C[e] = C[e’].

These are all the ingredients needed to understand the idea of “calculating with functions.”

1.5 Redex: Contexts, Reductions, Graphs

Let’s extend our language with contexts:
(define-extended-language Lambda-calculus Lambda
  (C ::=
     hole
     (lambda (x) C)
     (C e)
     (e C)))

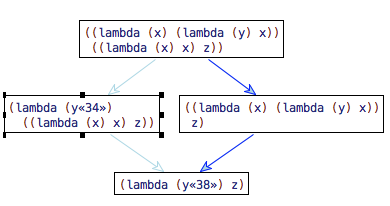
And let’s express the simple-minded beta relation as a relation on this calculus:
(define ->beta
  (reduction-relation
   Lambda-calculus
   #:domain e
   (--> (in-hole C ((lambda (x) e_1) e_2))
        (in-hole C (substitute e_1 x e_2))
        beta-name)))

There are two tools to explore this “calculus” now. The apply-reduction-relation function takes a step at a time:

(apply-reduction-relation ->beta (term (,e1 ,e2)))

Its cousin, apply-reduction-relation*, computes the transitive and reflexive closure but not the symmetric one.

Redex also comes with a tool that shows the reduction graph, that is, all reductions possible starting from some term until no more reductions can be applied:
(define e3
  (term
   ((lambda (x) (lambda (y) x))
    ((lambda (x) x) z))))
 
(traces ->beta e3)

Here is the result:

1.6 Theory: From Calculation to Programming Languages

(1) Programming language people are primarily interested in evaluating programs, and secondarily in reasoning about evaluation. Calculations supports both. It is good for the latter but is really miserable for the former—because it requires search through a graph to find the result. Fortunately, mathematicians prove (meta)theorems, and programming language people know how to exploit those.

Theorem If e relates to e’ in a reduction graph, then there exists a path of a particular shape. On this path, it is always the leftmost-outermost reducible expression (redex) that is reduced.

It turns out that this theorem holds for any sensible basic notion of reduction: beta-y, beta-z and something called beta-need, which we did not discuss.

Corollary An evaluator follows this path up to the first value (function, closure).

Here is now we say “leftmost-outermost” for beta-y and beta-z using context notation:

E-y = [] | (E-y e)

E-z = [] | (E-z e) | ((λx.e) E-z)

(2) Sensible programming language people do not want to encode numbers and booleans and strings, they want to work with them directly. Let’s add numbers and the most primitive operation on them: if. Here we go:

e = x | (λx.e) | (e e) | tt | ff | (if e e e)

This means we need two more relations and we need to union those with our favorite beta relation:

(if tt e e’) if-tt e

(if ff e e’) if-ff e’

In the literature, you will find the name δ reduction for these things or (external) interpretation function.

Numbers are a bit more complicated:

e = x | (λx.e) | (e e) | <n> for all n in Integer | (e + e)

The notation <n> is called a numeral, a syntactic representation of the number n. When we write <n + 1> we are referring to the numeral that represents the successor of numeral <n>. So here is the δ reduction for numbers:

(<n> + <m>) arithmetic <n + m>

1.7 Redex: Evaluators for Programming Languages

Let’s use evaluation contexts instead of plain contexts:
(define-extended-language Lambda-calculus Lambda
  (E-name ::=
     hole
     (E-name e)))
And here is the evaluator:
(define-metafunction PCF-eval
  eval : e -> v
  [(eval e) ,(first (apply-reduction-relation* ->beta (term e)))])
An evaluator is a function from terms to values. This definition glosses over some problems, which we will cover in the afternoon session.

(define-language PCF
  (e ::=
     x
     (lambda (x) e)
     (e e)
 
     ; booleans
     tt
     ff
     (if e e e)
 
     ; arithmetic
     n
     (e + e))
  (n ::=
     integer)
 
  (x ::= variable-not-otherwise-mentioned)
 
  #:binding-forms
  (lambda (x) e #:refers-to x))
 
(define-extended-language PCF-eval PCF
  (E-name ::=
     hole
     (E-name e)
     (E-name + e)
     (v + E-name))
  (v ::=
     n
     tt
     ff
     (lambda (x) e)))
Stop! Can you spot the bug in this definition?

And here are the reductions:
(define ->name
  (reduction-relation
   PCF-eval
   #:domain e
   (--> (in-hole E-name ((lambda (x) e_1) e_2))
        (in-hole E-name (substitute e_1 x e_2))
        beta-name)
   (--> (in-hole E-name (if tt e_1 e_2))
        (in-hole E-name e_1)
        if-tt)
   (--> (in-hole E-name (if ff e_1 e_2))
        (in-hole E-name e_2)
        if-ff)
   (--> (in-hole E-name (n_1 + n_2))
        (in-hole E-name ,(+ (term n_1) (term n_2)))
        plus)))

Time to get your hands dirty.

1.8 Summary: Theory

notation

     

meaning

x

     

basic notion of reduction, without properties

-->x

     

one-step reduction, generated from x, compatible with syntactic constructions

-->>x

     

reduction, generated from -->x, transitive here also reflexive

=x

     

“calculus”, generated from -->x, symmetric, transitive, reflexive

|–>x

     

standard reduction (one-step, multi-step), via meta-theorem

|–>>x

eval

     

functions, definable from -->>x, =x, or |–>>x

 

     

(equivalence from meta-theorems)

1.9 Summary: Redex

    ← prev  up  next →